Skip to main content

🎄 Trees

  • Trees has similar to the node structure of lists
  • The principal node is called Root
  • Below, we have the subtrees
  • Each node has a node pointing to him

Tree

🤔 Examples of uses​

  • HTML structure
  • Folders
  • Interfaces
  • RL example: a tree.
  • All nodes has 0 or more children
  • All nodes has just one father
  • The node degree is defined by the number of children what he have
  • Nodes with the same father are brothers
  • Nodes with degree zero can be called leaf
  • Path: A sequence of nodes. The size of this path is the number of arcs
  • Depth: To each node of a tree, exists a unique path between root and this node. The size of this path is called Depth.
  • Height: The depth max in any node

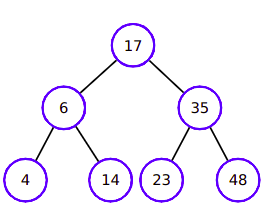
Types of Search

  • Post order: left -> right -> root (down to up)
  • Pre order: root -> left -> right (hierarchy)
  • In order: left -> root -> right (crescent)

Binary Tree

  • A binary tree has bellow each node, maximum of 2 subtrees.
  • Each node has 1 key and 2 pointers, one for the subtree in left and one for subtree in right

Ordering Tree

AVL Tree

  • This method is used to auto balancing the trees with rotations, making the module of heightLeft - heightRight be less than 1 (balanced). In AVL trees, we register the node height.

  • Right rotation: The left subtree is heavy

  • Left rotation: The right subtree is heavy

  • Left Right rotation: The Node heavy in left and subtree heavy in right. Makes a left rotation and a right rotation.

  • Right Left rotation: The node heavy in right and subtree heavy in left. Makes a right rotation and a left rotation.

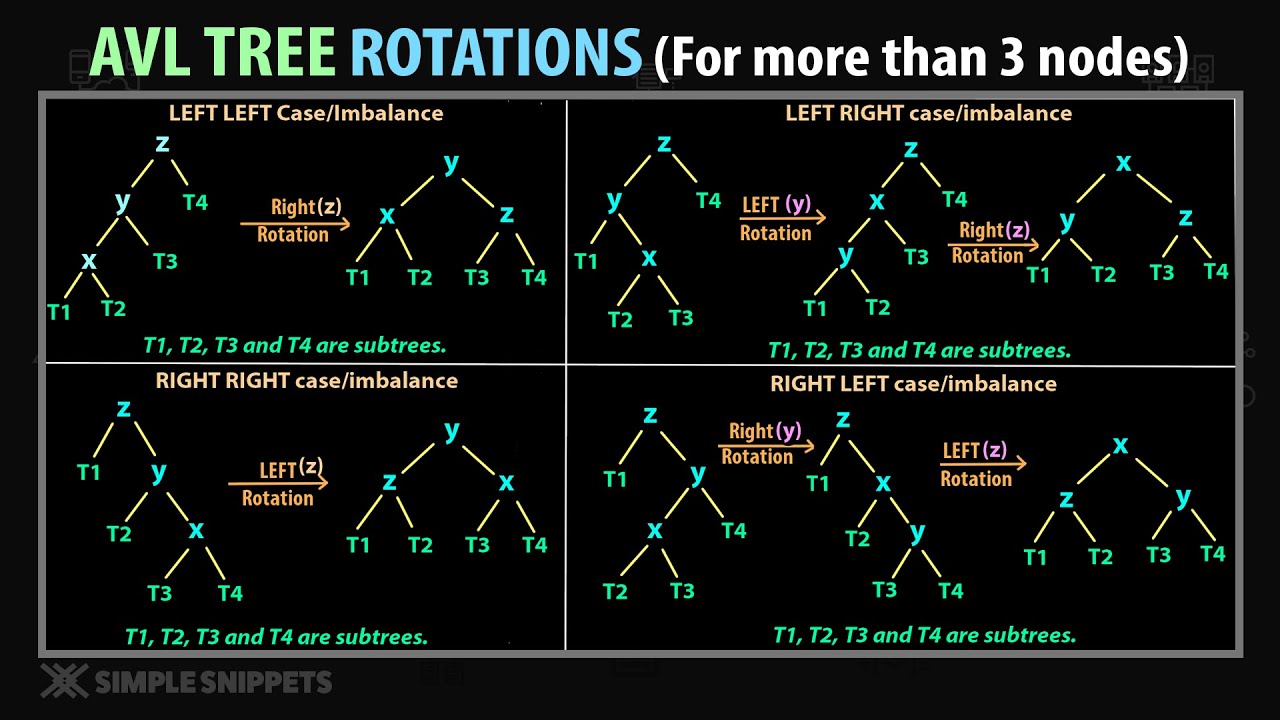
Tree Avl Rotations

Being B the Imbalance Factor (leftHeight - rightHeight):​

  • B > 1 and key < root.left.key: Right rotation.
  • B < -1 and key > root.right.key: Left rotation.
  • B > 1 and key > root.left.key: Left Right rotation.
  • B > -1 and key < root.right.key: Right Left rotation.