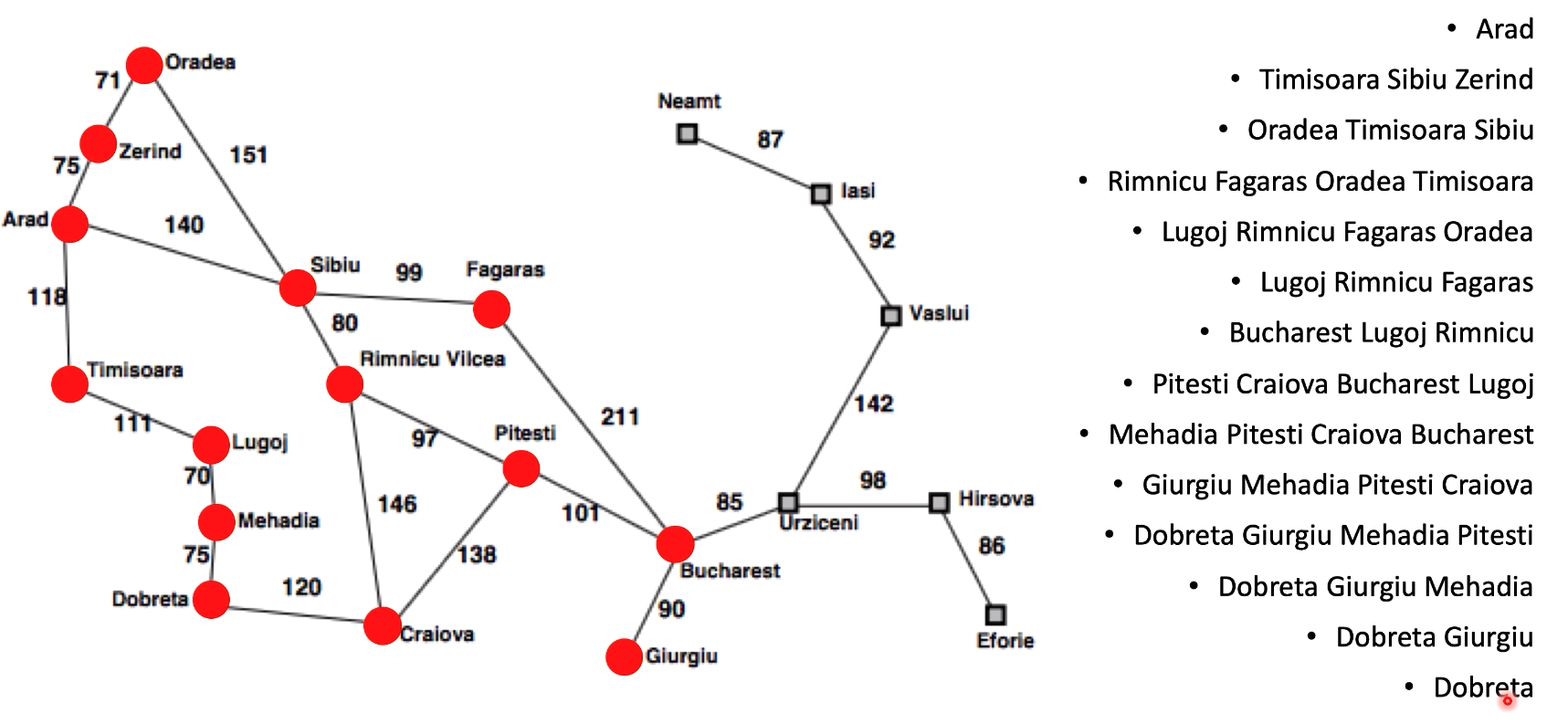
🌐 Graphs
- Abstract data type, made by a even V, E, with V being Vertices and E being Edges
- Could be Directed or Digraph when Edges has directions
- Could be No directed with no directions
- Edges can have weight
- Order: Number of vertices
🤔 Examples of uses
- Social media (like Facebook)
- Maps
- Web pages
- Subway
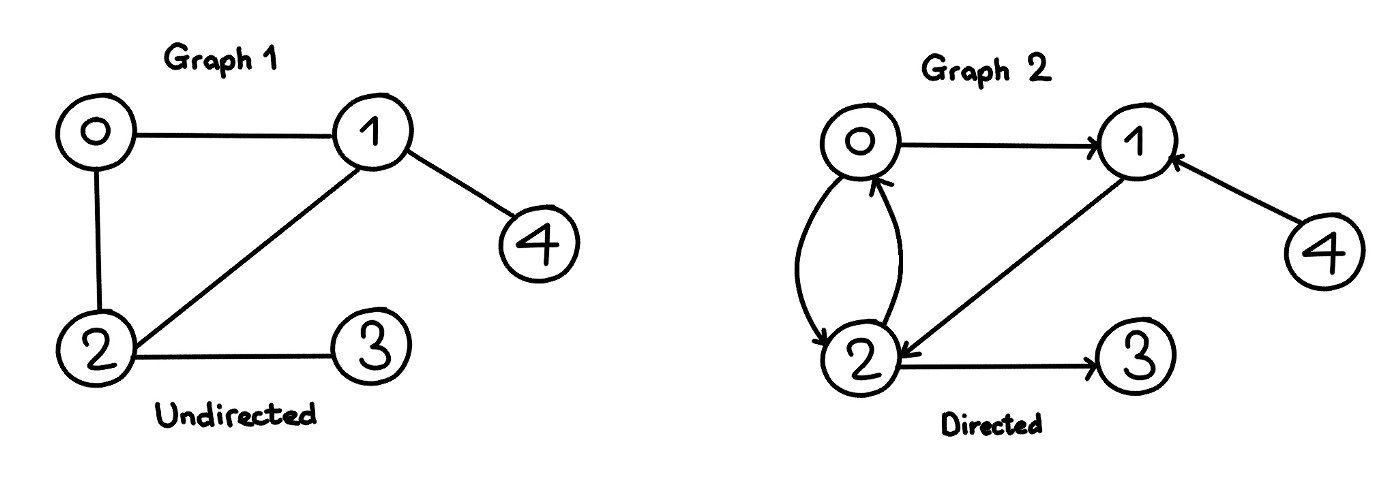
Graphs directed
- Connection output -> Adjacents
- If has connections, the elements connected are called neighbors
- Grade of a vertice it's the number of edges leaving the vertex + number of edges that arrive at the vertex
(adjacents vertices)
- It's strongly connected if each edge can be reachable from any other
Graphs not directed
- Symmetrical
- Grade of a vertice it's the number of edges that affect him (adjacents vertices)
- Is connected if each pair of vertices is connected by a path.
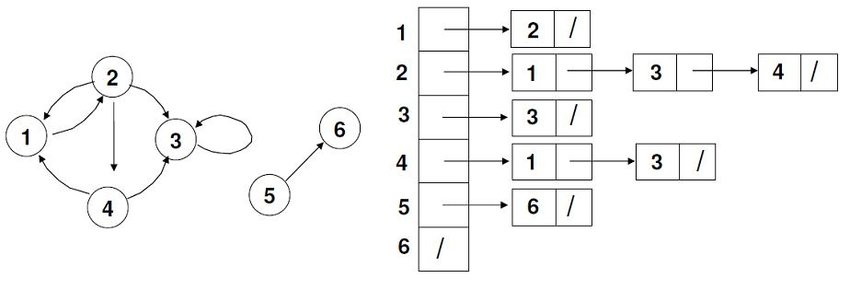
Adjacency list
- Stack of linked lists with all the adjacents vertices.
- Disadvantage: to know if a Edge (u, v) exists, we need to make a search in the list of adjacents.
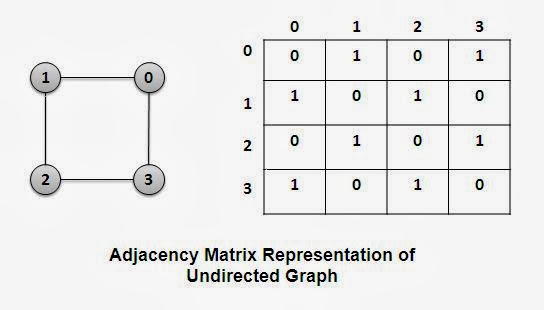
Adjacency matrix
- Best to small graphs
- Use a matrix format, with a V x V dimension (Vertice x Vertice)
- 1: adjacency with the value
- 0: no adjacency with the value
Searchs
Depth-First Search - Stack
- Similar to pre-order search in trees
- Visit a adjacent node not visited and push him on the stack.
- If has not adjacents not visited, pop the value
- If Rule 1 and Rule 2 is not the case, the search is finished.

Breadth-First Search - Queue
- Visit a adjacent not visited, mark and push on the queue.
- If has not a adjacent node, dequeue
- If Rule 1 and Rule 2 is not the case, the search is finished.