🧐 Big O - Asymptotic Complexity (O(x))
All code has a complexity, like:
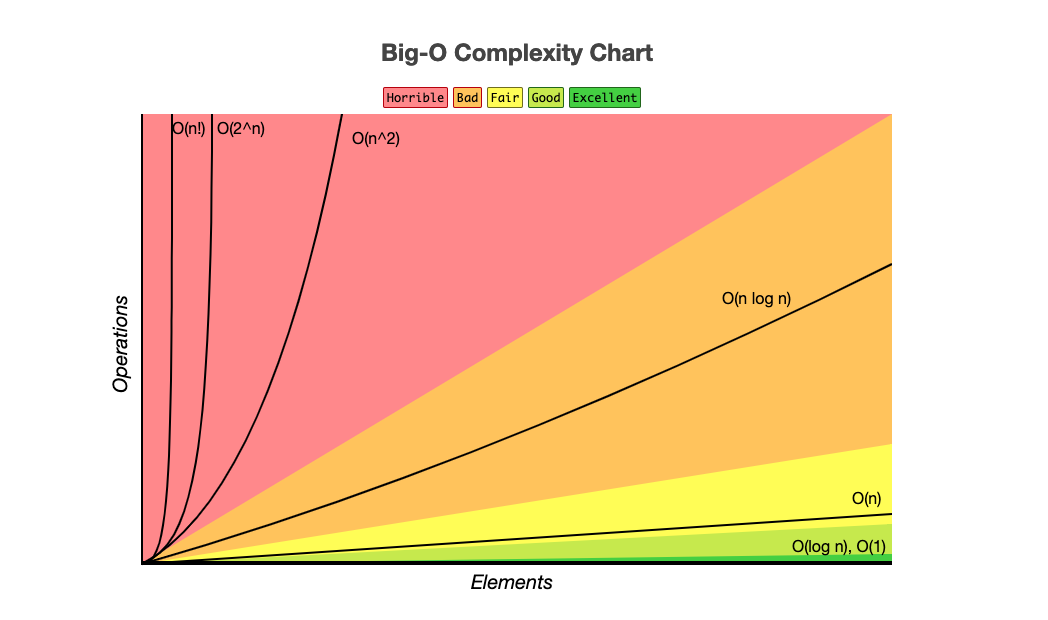
O(log n) - Logaritmics → Performatic, option to loop performatively. Example: binary search.
O(1) - Constant -> Complexity doesn't change independent of the input param. Example:
IFO(n) - Linear → More values, less performance. Example:
FOR.O(n²) - Exponencial → Repetition inside repetition. Will repeat each element again. Example:
FORinsideFOR.O(n³)
O(2^n)
O(3^n)
O(n!) - Fatorial -> The worst. Example: Recursive function.
| Big O Notation | Type | Computations for 10 elements | Computations for 100 elements | Computations for 1000 elements |
|---|---|---|---|---|
| O(1) | Constant | 1 | 1 | 1 |
| O(log N) | Logarithmic | 3 | 6 | 9 |
| O(N) | Linear | 10 | 100 | 1000 |
| O(N log N) | n log(n) | 30 | 600 | 9000 |
| O(N^2) | Quadratic | 100 | 10000 | 1000000 |
| O(2^N) | Exponential | 1024 | 1.26e+29 | 1.07e+301 |
| O(N!) | Factorial | 3628800 | 9.3e+157 | 4.02e+2567 |
Data Structure Operations Complexity
| Data Structure | Access | Search | Insertion | Deletion | Comments |
|---|---|---|---|---|---|
| Array | 1 | n | n | n | |
| Stack | n | n | 1 | 1 | |
| Queue | n | n | 1 | 1 | |
| Linked List | n | n | 1 | n | |
| Binary Search Tree | n | n | n | n | In case of balanced tree costs would be O(log(n)) |
| AVL Tree | log(n) | log(n) | log(n) | log(n) |